Black Hole Physics
Black holes are the most extreme objects predicted by Einstein’s relativity, enveloped in an event horizon and producing large distortions in the surrounding spacetime. These distortions are of particular current interest, because in dynamical situations (such as oscillating or orbiting black holes) they result in propagating gravitational waves. Inspiralling black holes are the strongest potential signal source of gravitational waves to be detected by ground-based interferometers, such as LIGO, GEO600 and Virgo . It is important to have accurate models of such inspirals for both the detection, and also the understanding, of the signals from these detectors.
. It is important to have accurate models of such inspirals for both the detection, and also the understanding, of the signals from these detectors.
Our work is focussed on understanding the dynamics of black holes through computer simulation of binary inspirals. This involves studying horizon dynamics and extracting gravitational wave information from physically realistic models.
-
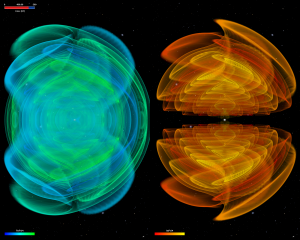
Calculation of gravitational waveforms: In order to detect gravitational waves and characterise their sources, accurate theoretical models are required. We use the Llama and Whisky codes to produce highly accurate waveforms which can then be used to generate waveform templates for various sources, against which experimental data will be compared.
-
Nonlinear black-hole physics: Recent work in Numerical Relativity has been focused on the generation of gravitational waves, but
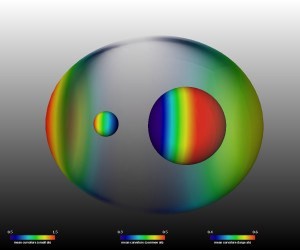 black holes are fascinating objects in their own right. When two generic black holes inspiral and merge, the anisotropic emission of linear momentum carried by the waves causes a “kick” to the final black hole that is produced. We study this because it is important astrophysically for understanding the ejection of supermassive black holes from galaxies in galaxy mergers. We are also studying the properties of the black hole horizons, the surfaces beyond which nothing, not even light, can escape, as well as the nonlinear dynamics of the geometry of a binary black hole spacetime.
black holes are fascinating objects in their own right. When two generic black holes inspiral and merge, the anisotropic emission of linear momentum carried by the waves causes a “kick” to the final black hole that is produced. We study this because it is important astrophysically for understanding the ejection of supermassive black holes from galaxies in galaxy mergers. We are also studying the properties of the black hole horizons, the surfaces beyond which nothing, not even light, can escape, as well as the nonlinear dynamics of the geometry of a binary black hole spacetime.
-
Formulation of the Einstein equations: There are many different ways to write Einstein’s equation as a time-evolution partial differential equations. Each of these formulations has different mathematical properties, and some are more amenable to numerical solution than others. We have recently derived a new formulation, the CCZ4 formulation, that has been shown to reduce numerical errors.
-
EM counterparts to SMBHs mergers: When supermassive black holes (SMBHs) merge in the presence of gas and magnetic fields, they emit not only gravitational waves, but also traditional electromagnetic radiation, for example X-rays. These electromagnetic counterparts to gravitational wave signals might be useful for more accurately determining the sky location of a gravitational wave source. We study the relation of the EM radiation to the black hole motion and the gravitational waves for various magnetic field configurations.